Berechnungprinzip
Das Prinzip der Stabilitätsberechnung der Felsböschung für eine polygonale Gleitfläche ist in den folgenden Abbildungen dargestellt.
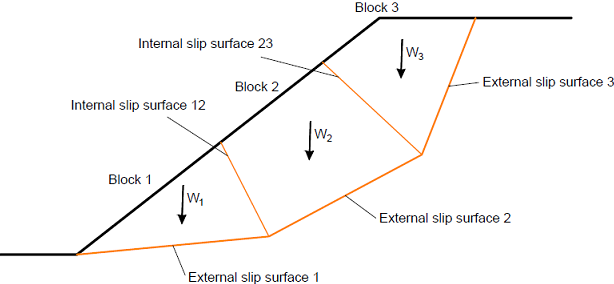 Schema der Felsböschung
Schema der Felsböschung
Die Berechnung wird sequentiell für alle Blöcke vom Block mit der höchsten Nummer bis zum Block Nr. 1 durchgeführt. Die Stabilität wird an jedem Block in Bezug auf den erforderlichen Sicherheitsfaktor geprüft und die auf den nächsten Block übertragenen Kräfte werden berechnet. Der niedrigste Stabilitätswert, der für alle Blöcke berechnet wurde, wird als resultierende Stabilität der Felsböschung dargestellt.
Der Vektor Di, der die Resultierende aller auf den Block i einwirkenden Kräfte darstellt, ist gegeben durch:
![]()
wo: | Wi | - | Resultierende des Eigengewichts des Gesteinsblocks |
Pi | - | Resultierende der äußeren auf den Block wirkenden Belastungen | |
Ei | - | Resultierende der Kräfte aufgrund des Erdbebens | |
Ui | - | Resultierende des Wasserdrucks, der auf die äußere Scherfläche einwirkt | |
Vi | - | Resultierende des Wasserdrucks, der auf die Trennflächen einwirkt | |
Hi | - | Kraft wegen der Auflast des Blocks durch Wasser über dem Gelände | |
Bi | - | Resultierende der Ankerkräfte auf dem Block |
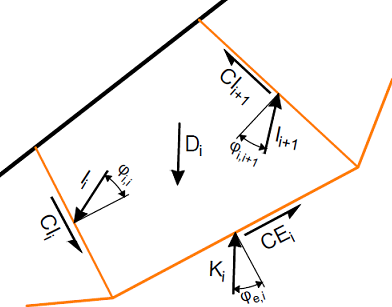 Schema der auf den Block wirkenden Kräfte
Schema der auf den Block wirkenden Kräfte
wo: | D | - | Resultierende aus allen äußeren Kräften, die auf den Block wirken |
CI | - | Resultierende der Kohäsion auf der inneren Scherfläche | |
CE | - | Resultierende der Kohäsion auf der äußeren Scherfläche | |
I | - | Reaktion zwischen der Blöcke auf der Trennfläche vom obersten Block | |
K | - | Reaktion auf der äußeren Scherfläche |
Um die Stabilität des Blocks i zu bemessen, wird die resultierende Kraft R bestimmt, die sich aus den auf den Block einwirkenden äußeren Kräften D und aus der vorherigen Blocks wirkenden Kräfte ergibt:
![]()
Wenn die Zugspannung an der äußeren Gleitfläche aufgrund der Kraft R auftritt, wird die Stabilität des Blocks entlang der innere Scherfläche überprüft.
![]()
![]()
wo | Ti | - | resultierende Widerstandskraft |
φi | - | Reibungswinkel auf der innere Scherfläche | |
RN,i | - | Normalkomponente der resultierende Kraft R | |
RT,i | - | Scherkomponente der resultierende Kraft R | |
CIi | - | Resultierende der Kohäsion auf der Scherfläche |
Wenn die Kraft R Druck auf die äußere Scherfläche wirkt, wird der Stabilitätsgrad FS gesucht, für den das Gleichgewicht der auf den Block einwirkenden Kräfte unter der Annahme, dass keine Spannung vorliegt, erfüllt ist. Zu der Kraft R werden die Resultierende der Kohäsion an der inneren und äußeren Scherfläche addiert und die resultierende Kraft muss mit den Reaktionen I und K im Gleichgewicht sein. Die Steigungen der Kräfte I und K sind durch die inneren Reibungswinkel φM gegeben. Dabei:
![]()
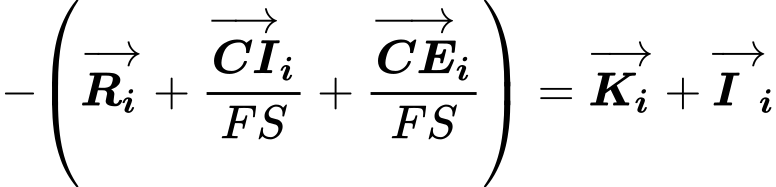
Der resultierende Stabilitätsgrad, für den die Gleichgewichtsbedingung erfüllt ist, wird dann mit dem gewünschten Sicherheitsfaktor SF verglichen.