Spencer法
Spencer法是根据极限平衡发展起来的一种通用条分法。它需要同时满足作用在各条块上的力和力矩的平衡条件。通过土条间接触面将滑面以上的土体划分为若干条块。作用在各条块上的力如下图所示。
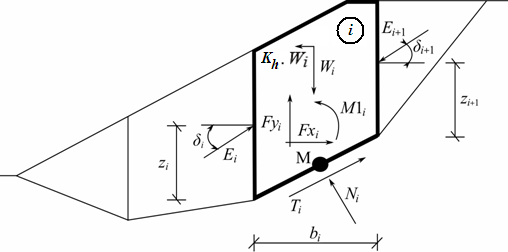静力图 – Spencer法
每个条块都假设承受以下作用力：
Wi | - | 条块重量，包括具有重量的实体超载并考虑了竖向地震加速度系数 Kv |
Kh*Wi | - | 反应地震作用的水平惯性力，Kh 是地震时的水平加速度系数 |
Ni | - | 滑面上的法向力 |
Ti | - | 滑面上的剪切力 |
Ei,Ei+1 | - | 条块间的作用力，与水平面的夹角为 δ |
Fxi,Fyi | - | 其它作用在条块上的水平或竖向力 |
M1i | - | Fxi, Fyi 对点M作用的力矩，点 M 为第 i 块条块对应滑面段的中心点 |
Ui | - | 第 i 块条块对应滑面段上的孔隙水压力合力值 |
为了求解各条块的极限作用力和力矩平衡方程组，在Spencer法中做出了如下假设：
- 各条块间的土条间接触面是垂直的
- 条块重量 Wi 的作用线穿过第 i 块条块对应滑面段的中心点，即 M 点
- 法向力 Ni 作用在第 i 块条块对应滑面段的中心点处，即 M 点处
- 所有条块受到的条块间作用力 Ei 的倾斜角度都是常量，都为 δ。只有在滑面两个端点处 δ=0
此方法中将使用到以下方程式：
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
方程（1）表示的是作用在滑面上的法向力有效应力值和总应力值之间的关系。方程（2）为表征某滑面段上法向力和剪切力关系的Mohr-Coulomb条件。方程（3）为第 i 滑面段法线方向上的作用力平衡方程，而方程（4）表示的是沿第 i 滑面段切线方向的受力平衡。SF 是安全系数，用来折减土的强度参数值。方程（5）对应的是条块上作用力关于点 M 取矩的力矩平衡方程，其中 ygi 是条块重力作用点的垂直坐标，yM 是点 M 的垂直坐标。整理方程（3）和（4）得到下列递归公式（6）：
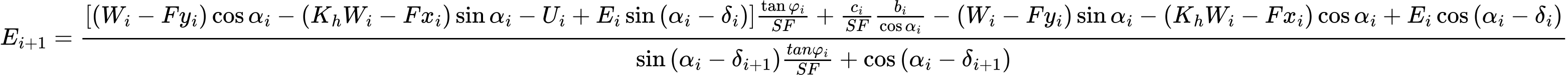
通过给定的作用力倾角值δi和安全系数值 SF，便可以根据该方程计算出条块间作用力Ei。且该方法假设坡脚条块左侧的作用力E等于零，即E1 = 0。
由力矩平衡方程式（5）得到另一个递归方程（7）：
对于给定的 δ 值，可以由上式计算得到所有条块间作用力的力臂值 z。其中坡脚条块左侧的力臂值z1=0 。
采用以下的迭代过程计算安全系数 SF：
- δ 的初始值设为 δ = 0。
- 假设坡顶条块右侧上的作用力 En+1 = 0，则对于给定的 δ 值，可以由方程式（6）得到安全系数 SF。
- 使用在前面步骤中确定的 E 值，根据坡脚条块上作用的合力矩值为 0 的条件，由方程式（7）求得一个新的δ值。方程（7）并没有给出 zn+1 的值，而是假设等于零。在此取值条件下，必须满足力矩平衡方程（5）。
- 重复步骤2和3，直到 δ 的值不再改变为止。
为了使迭代过程收敛，就必须避免不稳定解。当表达式（6）或（7）中的分母为零时便会出现这种不稳定求解的情况。在式（7）中，当 δ = π/2 或 δ = -π/2 时，分母为零。所以角 δ 的取值范围为(-π/2; π/2)。
当满足下式时，方程式（6）中的除数为零：
另一项防止迭代不稳定性的检查是对参数 mα 的验算 - 必须满足以下条件：
因此在迭代计算之前，必须找出满足上述条件的最小临界值（SFmin）。使用小于临界值 SFmin 的数值计算后会得到不稳定解，因此将 SF 设置为仅比 SFmin 大一微小增量的值进行迭代，从而保证迭代过程中得到的所有 SF 的值都大于 SFmin。
一般而言，严格的计算方法比简单方法（Bishop、Fellenius）的收敛性要差。存在收敛问题的情况有：滑动面区段太陡，几何模型复杂，超载突变等。如果得不到计算结果，建议稍微改变一下输入的数据，比如：滑面不要太陡，在滑面上确定更多的点位等。或者使用一些简单的分析方法。
参考文献：
Spencer, E. 1967. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique, 17(1): 11–26.