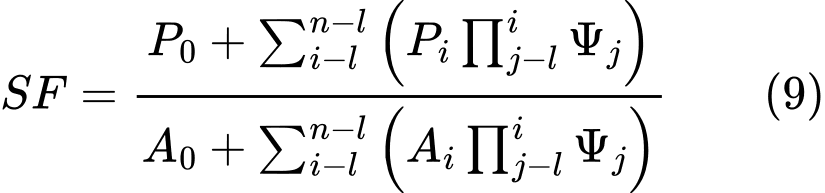Metoda ITF (Imbalance Thrust Force Method)
Metoda ITF jest metodą stanów granicznych. W metodzie tej budowane jest równanie równowagi sił oddziałujących na poszczególne bloki, natomiast nie uwzględniane jest równanie równowagi momentów. Podstawoe zasady oraz założenia tej metody zaprezentowano na schemacie poniżej:
 Rys. 1 Siły oddziałujące na blok - metoda ITF
Rys. 1 Siły oddziałujące na blok - metoda ITF
Poniższe założenia zostały przyjęte w odniesieniu do sił oddziałujących na blok:
gdzie: | Wi | - | ciężar itego bloku, ciężar części bloku gruntu poniżej zwierciadła wody gruntowej wyznaczany jest na podstawie ciężaru gruntu nawodnionego γsat |
Fyi | - | reprezentuje pozostałe obciążenie pionowe oddziałujące na blok | |
Fxi | - | reprezentuje pozostałe obciążenie poziome oddziałujące na blok | |
Fi, Fi+1 | - | ssiły oddziałujące między blokami wzdłuż kierunków zdefiniowanych za pomocą kątów αi oraz αi+1 |
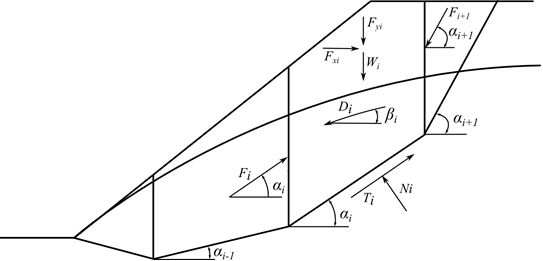
 Rys. 2 Schemat oddziaływania ciśnienia porowego na blok
Rys. 2 Schemat oddziaływania ciśnienia porowego na blok
Ui | - | wypadkowa ciśnienia porowego na segment powierzchni poślizgu | |
UVi,UVi+1 | - | wypadkowe ciśnienia porowego na płaszczyzny pomiędzy blokami |
Siły UVi i UVi+1 są zawarte w poziomych siłach Fxi.
Równanie równowagi sił w kierunku normalnym do segmentu powierzchni poślizgu określa:
![]()
Siły na segment powierzchni poślizgu są powiązane ze sobą poprzez
![]()
gdzie: | φi | - | kąt tarcia wewnętrznego gruntu |
ci | - | spójność gruntu | |
li | - | długość segmentu powierzchni poślizgu powiązana z itym blokiem |
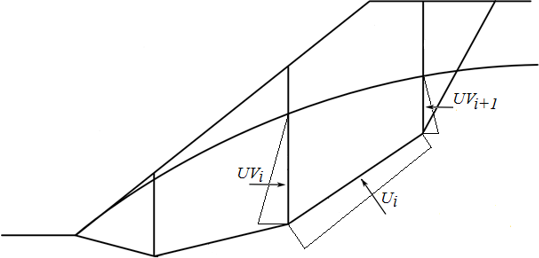
Równanie równowagi sił w kierunku itego segmentu powierzchni poślizgu (określonego przez kąt αi) opisuje siłę Fi oddziałującą między blokami jako:
![]()
Wprowadzając równania (1) oraz (2) do równania (3) otrzymujemy:
oraz po pewnych przekształceniach algebraicznych uzyskuje się następującą formę równania równowagi sił:
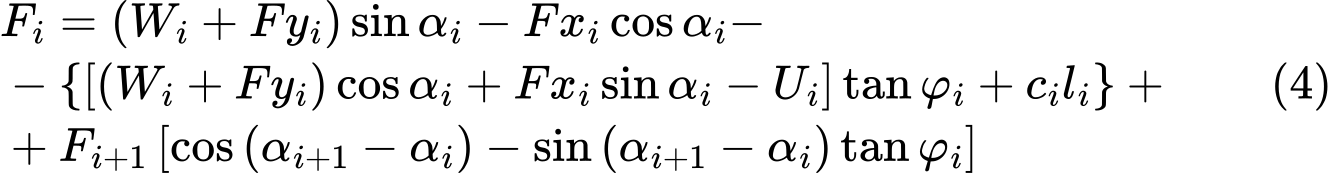
Warunek równowagi będzie spełniony po wprowadzeniu do obliczeń współczynnika bezpieczeństwa SF takiego, że parametry wytrzymałościowe danego gruntu c oraz tanφ są dzielone przez tę wartość. Równanie (4) otrzymuje wówczas formę:
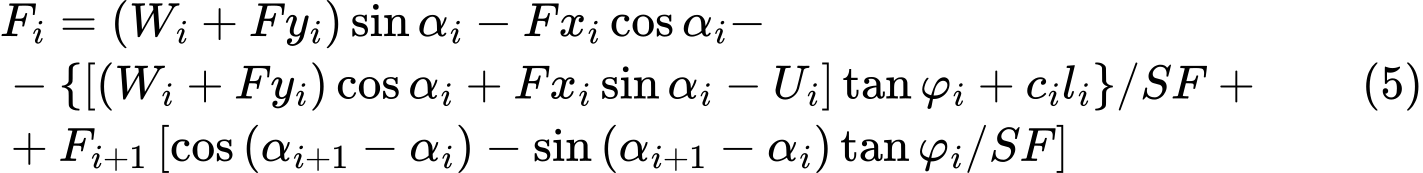
Następnie, poprzez proces iteracji, z równania (5) uzyskuje się poszukiwany współczynnik bezpieczeństwa SF. Proces ten przeprowadzany jest w taki sposób, że siła Fn równa 0 kN przykładana jest w najwyższym (końcowym) punkcie powierzchni poślizgu. Siły Fi oddziałujące pomiędzy blokami, wyznaczane są dla zadanej wartości współczynnika bezpieczeństwa SF z równania (5). Krok ten powtarzany jest dla wielu wartości współczynnika SF aż do momentu, gdy znaleziony zostanie taki współczynnik bezpieczeństwa SF, dla którego siła F0 w podstawie zbocza staje się równa 0 kN. Nie zakłada się rozciągania wzdłuż powierzchni poślizgu. W przypadku, gdy warunek równowagi wymaga ujemnej wartości siły normalnej Ni, co oznacza, że grunt jest rozciągany, wówczas w następnym kroku iteracji wartość tej siły jest przyjmowana jako zero, a siła tnąca Ti oddziałująca na dany segment wyznaczana jest wyłącznie na podstawie spójności gruntu.
Metoda ITF jest stosunkowo wrażliwa na kształt powierzchni poślizgu. W przypadku, gdy powierzchnia poślizgu zawiera ostre nieciągłości segmentów wyznaczony z obliczeń współczynnik bezpieczeństwa jest wyższy od rzeczywistego. Zaleca się aby różnica pochyleń sąsiadujących ze sobą segmentów powierzchni poślizgu nie była większa niż 10°. Warunek ten jest automatycznie weryfikowany przez program. Jeśli różnica nachyleń segmentów jest znacznie większa od zalecanej pojawia się ostrzeżenie, że wyniki obliczeń mogą być przeszacowane. Zwykle problem ten nie dotyczy kołowej powierzchni poślizgu, powinien jednak być uwzględniany w przypadku powierzchni łamanych.
Metoda ITF - jednoznaczne rozwiązanie
Rozwiązanie jednoznaczne metody ITF zakłada odmienną metodę wprowadzania współczynnika bezpieczeństwa do obliczeń. Wówczas rozwiązanie matematyczne nie wymaga iteracji a wynikowy współczynnik bezpieczeństwa wyznaczany jest bezpośrednio w pojedynczym kroku obliczeniowym. Stosując takie podejście uzyskuje się zwykle wyższe współczynniki bezpieczeństwa. Obniża to znacząco wartość tego rozwiązania, szczególnie w przypadku zastosowania także łamanej powierzchni poślizgu ze znaczącymi różnicami nachylenia sąsiednich segmentów.
Rozwiązanie wykorzystuje równanie (4), do którego wprowadzany jest wsółczynnik bezpieczeństwa SF taki, który przemnaża aktywne składowe sił, tj. składowe oddziałujące w kierunku przesuwającym. Warunek równowagi przyjmuje postać:
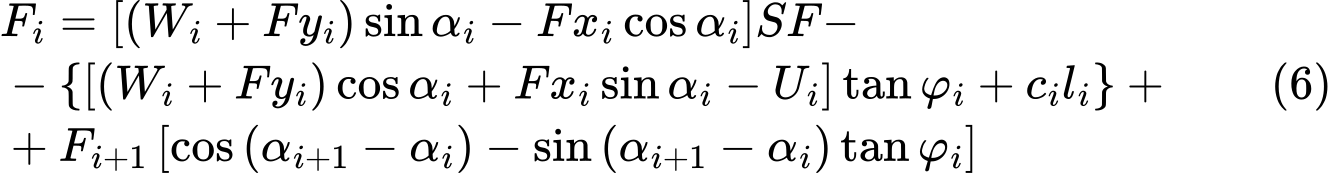
Dla przejrzystości wprowadzamy składowe sił aktywnych w postaci:
![]()
a następnie składowe sił biernych jako:
![]()
oraz funkcję pomocniczą:
![]()
Równanie (6) może być zapisane w bardziej kompaktowej formie w postaci:
![]()
W następnym kroku zakłada się znaną siłę Fn = 0 w celu zapisania wyrażeń sił pomiędzy blokami F w postaci:
![]()
![]()
![]()
itd.
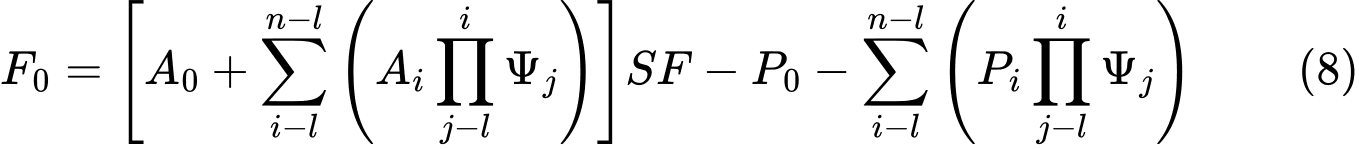
Ostatecznie, zakładając, że siła oddziałująca na dolny początek powierzchni poślizgu ma być równa 0 kN, otrzymuje się końcową postać współczynnika bezpieczeństwa SF: