Surface de glissement polygonale
La résolution du problème de stabilité des pentes en adoptant une surface de glissement polygonale est basée sur la détermination de l'état limite des forces agissant au dessus de la surface de glissement. Pour introduire ces forces, la surface de glissement est subdivisée en blocs par des plans de division. Classiquement ces plans sont supposés verticaux, mais ce n'est pas une obligation, par exemple la méthode de Sarma utilise généralement des plans inclinés.
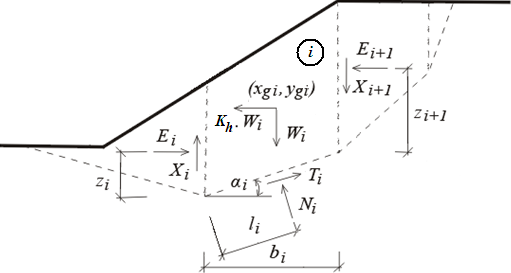Schéma statique de bloc
La figure ci-dessus montre les forces agissant sur les blocs de sol individuels. Si la région au dessus de la surface de glissement est divisée en bloc, alors pour le calcul des inconnues nous avons : n forces normales Ni agissant sur les segments individuels et correspondant à n forces de cisaillement Ti ; n-1 forces normale entre les blocs Ei et correspondant à n-1 forces de cisaillement Xi ; n-1 valeurs de zi représentant les points d'application des forces Ei ; n valeurs de li représentant les points d'application des forces Ni et une valeur pour le coefficient de sécurité SF. Les forces Xi peuvent, dans certaines méthodes, être remplacées par les valeurs de l'inclinaison des forces Ei.
Pour résoudre le problème d'équilibre, nous avons l'ensemble d'équations suivant : n équations horizontales et n équations verticales d'équilibre pour les blocs individuels, n équations d'équilibre de moment pour les blocs individuels et n relations entre les forces Ni et Ti développées sur les blocs selon la théorie de Mohr-Coulomb. Au total, il y a 4n équations pour 6n-2 inconnues. Ce qui suggère que 2n-2 inconnues doivent être valorisées au préalable. Les méthodes individuelles diffèrent des autres par le fait que ces valeurs sont choisies.
Le plus souvent les points d'application des forces agissant entre les blocs ou leurs inclinaisons sont choisis. La résolution du problème d'équilibre se fait itérativement, les valeurs choisies devant permettre de satisfaire à la fois l'admissibilité de l'équilibre et l'admissibilité cinématique de la solution obtenue.
Le programme permet d'utiliser l'une des méthodes suivantes :
L'optimisation de la surface de glissement polygonale recherche la surface la plus critique (celle donnant le coefficient de sécurité le plus petit).