Ayuda en línea

Argile hypoplastique

L’argile hypoplastique s’applique à la modélisation de sols tendres à grains fins. Comme tous les autres modèles, il appartient à la famille des modèles phénoménologiques standards. Quant à la description de la réponse du sol, elle relève du groupe des modèles d'état critique (Cam-Clay, Cam-Clay généralisée). Ce modèle, cependant, rend compte de la réponse non linéaire des sols à la fois en chargement et en déchargement. Comparé à d'autres modèles basés sur la théorie de la plasticité, il ne permet de calculer que les déformations totales. Il ne fait donc aucune différence entre les déformations élastiques et plastiques. La nature de la rupture, représentée par la région de déformation plastique équivalente localisée dans les modèles standards, peut être représentée, par exemple, par la distribution de l'angle de frottement interne mobilisé pour l'argile hypoplastique.

Afin de décrire la réponse du sol, le modèle permet de restituer une rigidité différente lors du chargement et du déchargement, du ramollissement ou du durcissement en fonction du compactage du sol et de la variation de volume en cisaillement (dilatance, compression). La rigidité courante dépend uniquement de la direction de la charge, mais également de l'état courant du sol donné par sa porosité. Contrairement aux modèles Cam-Clay, il exclut strictement les contraintes de traction dans le sol, voir la figure 1a.

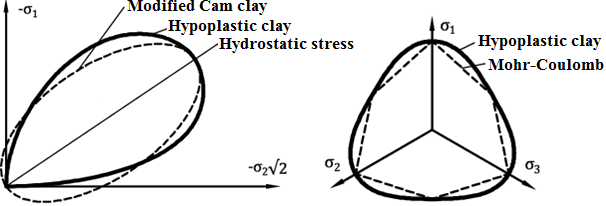Figure 1: Limite des états du modèle hypoplastique - (a) comparaison avec la surface de limite élastique du modèle Cam-Clay dans le plan méridien, (b) comparaison avec la surface de limite élastique du modèle de Mohr-Coulomb dans le plan déviatorique

Concernant le modèle hypoplastique, la surface de limite élastique standard est remplacée par la surface dite à l'état limite. Sa projection dans le plan déviatorique est similaire au modèle, voir la figure 1b. La règle d'écoulement n'est pas associée, ce qui donne une matrice de rigidité non symétrique (à comparer, par exemple, avec le modèle de Mohr-Coulomb lorsque différentes valeurs sont données pour l'angle de frottement interne φ et l'angle de dilatance ψ). Des détails concernant la formulation du modèle peuvent être trouvés dans la référence [1].

Paramètres du modèle

La variante élémentaire du modèle nécessite la saisie de cinq paramètres de matériau :

• Angle de frottement interne à volume constant (angle critique de frottement interne) φ_cv
• Pente de la ligne de gonflement κ*
• Pente de la ligne de consolidation normale (LCN) λ*
• Origine de la ligne de consolidation normale N
• Rapport du module unitaire sur le module de cisaillement r

Les paramètres κ*, λ* et N déterminent un diagramme bilinéaire de la consolidation isotrope sur une échelle log-log, Figure 2a. Si les paramètres du modèle Cam-Clay bilinéaire (à l’échelle semi-logarithmique, Figure 2b) sont disponibles, il est possible de saisir ces valeurs et les paramètres du modèle hypoplastique sont recalculés. Les paramètres du modèle Cam-Clay sont bilinéaires :

• Pente de la ligne de gonflement κ (en échelle semi-logarithmique)
• Pente de la ligne de consolidation normale λ (en échelle semi-logarithmique)
• Indice des vides e_max pour la consolidation isotrope normale par une pression de 1kPa

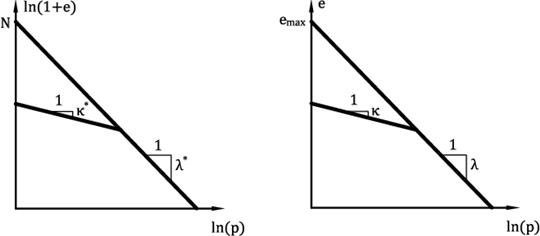Figure 2: Diagram bilinéaire de consolidation isotrope - (a) Argile hypoplastique, (b) Modèle Cam-Clay

Angle de frottement interne critique φ_cv

• Il est identique pour l'échantillon d'origine (non remanié) et pour l'échantillon reconstitué puis consolidé
• Il peut être déterminé à partir d'un essai triaxial standard appliquant différentes pressions de cellules sur un échantillon reconstitué
• Les essais drainés et non drainés (plus rapides) peuvent être effectués
• Les valeurs les plus courantes sont dans la fourchette 18° - 35°

Pente de la ligne de consolidation normale λ*

• Elle est déterminé graphiquement à partir de la phase de charge de l'essai œdométrique ou de l'essai de consolidation isotrope, voir Figure 3
• Pour les argiles raides, il est préférable d’effectuer l'essai sur un échantillon reconstitué
• Les valeurs les plus courantes sont dans la fourchette 0,04 - 0,15

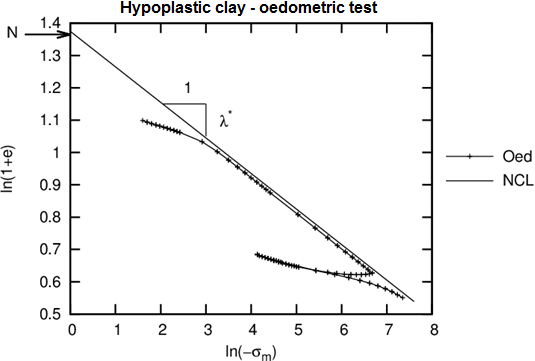Figure 3: Simulation d'essai œdométrique pour un modèle hypoplastique

Pente de la ligne de gonflement κ*

• Elle peut être déterminée graphiquement (comme pour λ*) ou en effectuant une étude paramétrique - en comparant les mesures et la simulation au cours du processus de déchargement de l'essai de consolidation œdométrique ou isotrope, voir Figure 3.
• Les valeurs les plus courantes de κ sont dans la fourchette 0,01 - 0,02
• Le rapport λ/κ devrait être plus grand que 4,0

Origine de la ligne de consolidation normale N

• Elle est déterminé graphiquement à partir de la phase de charge de l'essai œdométrique ou de l'essai de consolidation isotrope
• L'essai doit être effectué sur un échantillon non remanié - lors de la recherche de l'intersection de la ligne λ avec l'axe vertical, il est possible de déterminer la pente λ obtenue à partir d'un échantillon reconstitué, voir la figure 3.
• Les valeurs les plus courantes se trouvent dans la fourchette 0,8 - 1,6

Rapport du module unitaire sur le module de cisaillement r

• La signification physique de ce paramètre est donnée par l'expression r = K_i/G_i
• K_i correspond au module unitaire tangent de compression isotrope selon la ligne de consolidation normale
• G_i correspond au module de cisaillement tangent pour l'essai de cisaillement non drainé en supposant le même état de contrainte
• Le paramètre r peut être déterminé par une étude paramétrique de l'essai triaxial au cisaillement
• Les valeurs les plus courantes se trouvent dans la fourchette 0,05 - 0,7

Définition de l'état initial du sol

Dans l'argile hypoplastique, l'état courant du sol est associé au compactage courant représenté par l'indice des vides. La mise en œuvre du modèle permet de saisir l'indice des vides initial ou courant soit directement, soit de le recalculer à l’aide de la pression de préconsolidation saisie OCR. Dans le premier cas, la valeur saisie e₀ correspond à l'indice des vides mesuré sur un échantillon non chargé extrait à une profondeur donnée. Dans le second cas, la valeur saisie de e_curr correspond à l'indice des vides d'un sol soumis à des contraintes. Dans le dernier cas, la valeur de l'OCR est spécifiée. Ce paramètre représente le rapport entre la contrainte moyenne sur la LCN et la contrainte moyenne initiale, voir la figure 4b.

Lors de l'initialisation du calcul à l'aide de la procédure K_o, l'état de contrainte courant au début de la deuxième étape est affecté à l'état de contrainte courant. Si l’adoption d’une analyse standard lors de la première étape (le modèle de argile hypoplastique est introduit dès la première étape de calcul) où le sol est chargé par son poids propre, la valeur de la contrainte initiale p_in = 1 kPa est supposée et on a e_curr = e₀. Si un matériau différent (par exemple, un matériau élastique est pris en compte dans la première étape de calcul) est remplacé par le modèle d'argile hypoplastique, l'état initial de contrainte dérivé de l'étape précédente est adopté. On note que lorsque l'on utilise un matériau élastique dans la première étape de calcul, l'état de contrainte résultant correspond aux résultats fournis par la procédure K_o pour K_o (ν est le coefficient de Poisson).

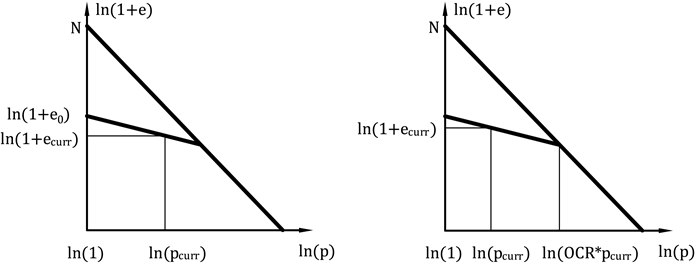Figure 4: Initialisation de l'indice des vides - (a) à l'aide de l'indice des vides initial, (b) à l'aide de l'OCR

La figure 5 montre clairement que, pour les sols normalement consolidés, l’état pour lequel OCR = 1,0 correspond à une consolidation isotrope uniquement, donc pour K_o = 1,0. Si le sol subit un état de contrainte déviatorique non nul, l’OCR correspondant à un sol normalement consolidé est supérieur à 1,0. Une valeur exacte de OCR_NC dépend à la fois des paramètres du sol et du chemin de contrainte (la valeur de K_o). La figure 5 montre la dépendance du minimum pour différentes valeurs de K_o et différents types de sols argileux. Des valeurs particulières sont également indiquées dans le tableau 1. Les caractéristiques élémentaires des matériaux de cet ensemble de sols sont répertoriées dans le tableau 2.

Le choix OCR = 1,0 pour les sols normalement consolidés avec K_o différent de 1,0 crée un état de contrainte non acceptable pouvant entraîner une perte de convergence.

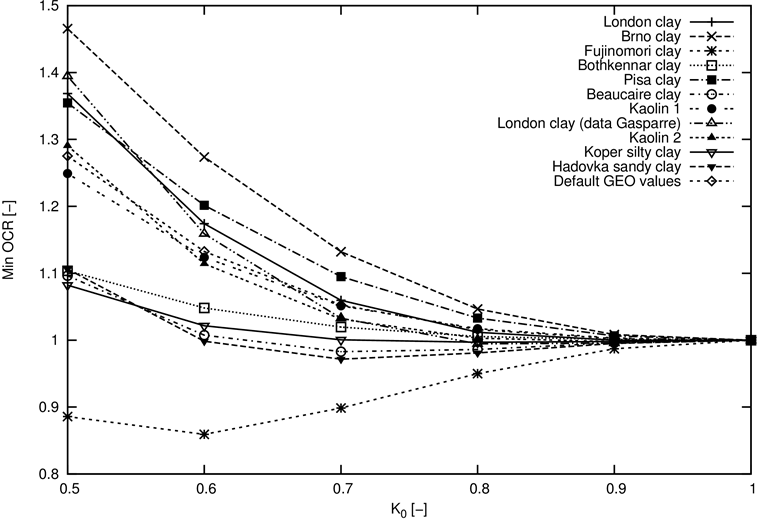Figure 5: Dépendance de l'OCR par rapport au coefficient de pression des terres au repos K_o

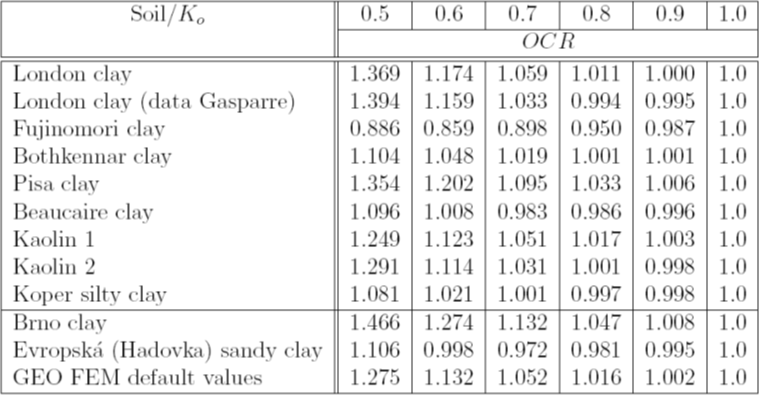Tableau 1: Indice de surconsolidation OCR des sols sélectionnés en fonction de la valeur de K_o

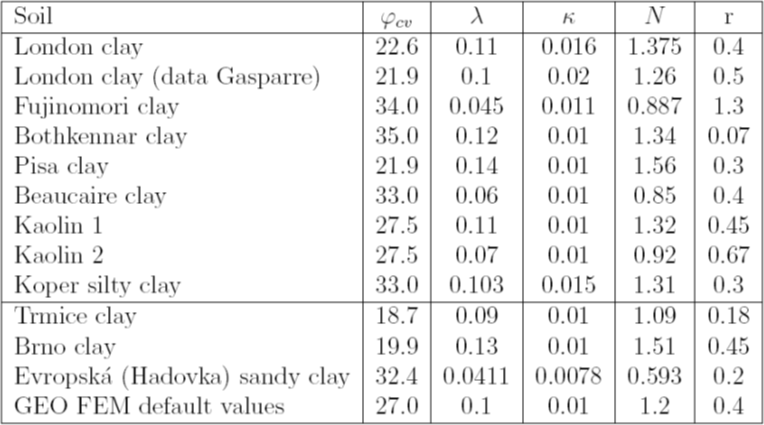Tableau 2: Caractéristiques matérielles des sols sélectionnés

Déformation intergranulaire

La version de base du modèle convient aux analyses présentant une direction prédominante du chemin de chargement de contrainte. Dans les cas de chargement cyclique (chargement-déchargement-rechargement), il est plus approprié d'utiliser la formulation avancée prenant en compte le concept de déformation intergranulaire. Cela permet de limiter une augmentation inacceptable de la déformation des éléments lors de petites modifications répétées de la charge (cliquet). L'introduction d'une déformation intergranulaire permet la modélisation de grandes rigidités que les argiles subissent lors de petites déformations. Cette option ne fait partie d'aucun autre modèle implémenté dans le programme MEF. Le concept de déformation intergranulaire suppose que la déformation totale du sol consiste en une petite déformation d'une couche intergranulaire (déformation intégranulaire) et en une déformation provoquée par le glissement mutuel des grains. Changer le chemin de la charge change d'abord la déformation intergranulaire. Lorsque la valeur limite de la déformation intergranulaire est atteinte, la déformation associée au mouvement des grains s’active.

Le choix du concept de contrainte intergranulaire nécessite cinq paramètres supplémentaires :

• Fourchette de déformation intergranulaire élastique R
• Paramètres m_R et m_T contrôlant la rigidité aux faibles déformations
• Paramètres β_r et χ contrôlant le degré de dégradation de la rigidité pour une déformation croissante

Ces paramètres sont calibrés avec les paramètres déjà connus du modèle hypoplastique de base.

Fourchette de déformation intergranulaire élastique R

• Elle détermine la gamme de déformation intergranulaire maximale
• Elle peut être déterminée par l'étude paramétrique de la courbe de dégradation G = G(ε_s), Figure 6
• Alternativement, elle peut être considérée comme une constante indépendante du matériau R = 10^-4
• Les valeurs les plus courantes sont dans la plage 2_*10^-5 - 1_*10^-4

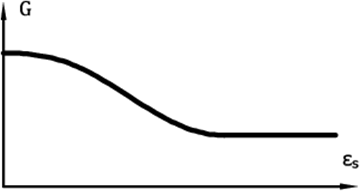Figure 6: Courbe décrivant la perte de rigidité du module de cisaillement

Paramètre m_R

• Il détermine l'intensité du module de cisaillement lors du changement du chemin de chargement dans le plan méridien (σ_m - J) o 180°
• Le rapport linéaire entre le paramètre m_R et le module de cisaillement initial G₀ est fourni par G₀ = p_*(m_r/(r_* λ*)
• Le module de cisaillement initial peut être déterminé à partir de la mesure de la propagation de l'onde de cisaillement [2].
• Les valeurs les plus courantes sont dans la plage 4,0 - 20,0

Paramètre m_T

• Il détermine l'intensité du module de cisaillement lors du changement du chemin de chargement dans le plan méridien (σ_m - J) o 90°
• On a m_R/m_T = G₀/G₉₀
• Le rapport des modules initiaux peut être estimé à partir du rapport de ces modules pour les plus grandes déformations. La valeur du rapport m_R/m_T est généralement comprise entre 1,0 et 2,0.
• Les valeurs les plus courantes de m_T sont dans la plage 2,0 - 20,0

Paramètres β_r et χ

• Ils déterminent le taux de dégradation de la rigidité lorsque la contrainte de cisaillement augmente
• Ils peuvent être déterminés par l'étude paramétrique de la courbe de dégradation G = G(ε_s)
• Les valeurs les plus courantes de β_r sont dans la plage 0,05 - 0,5
• Les valeurs les plus courantes de χ sont dans la fourchette 0,5 - 6

Littérature:

[1] D. Mašín, A hypoplastic constitutive model for clays, International Journal for Numerical and Analytical Methods in Geomechanics., 29:311-336, 2005.