Capacité portante horizontale - méthode de Broms
Les articles de 1964 donnés en référence décrivent la méthode d'analyse d'un pieu isolé selon Broms. Cette méthode suppose seulement que le pieu se trouve dans un sol homogène, les sols stratifiés s'en trouvent donc exclus. L'onglet "Pieux" du cadre "Paramètres" permet de choisir cette méthode.
Si la méthode de Broms est sélectionnée pour l'analyse de la capacité portante horizontale, le programme ne tient plus compte des couches de sol déjà introduites. Les paramètres du sol sont spécifiés dans le cadre "Capacité de charge horizontale" en fonction du type de sol (cohérent, pulvérulent).
Les paramètres d'entrée pour le calcul de la capacité portante horizontale du pieu sont les caractéristiques du matériau du pieu (module d'élasticité et de la résistance d'un matériau donné), la géométrie du pieu (longueur du pieu l et son diamètre d) ainsi que la charge du pieu due à la force de cisaillement et au moment de flexion.
Le coefficient de raideur du pieu β pour des sols cohérents est donné par la relation :
![]()
où : | EI | - | raideur en flexion du pieu [MNm2] |
kh | - | ||
d | - | diamètre du pieu [m] - pour un pieu de section circulaire variable, le diamètre de pieu d1 (saisi dans le cadre "Géométrie") est utilisé pour le calcul du paramètre β. |
Pour les sols pulvérulents le coefficient de raideur du pieu η est défini par la relation :
![]()
où : | EI | - | raideur en flexion du pieu [MNm2] |
nh | - | coefficient de réaction du sous-sol [MNm3] |
Le programme détermine automatiquement s'il faut considérer un pieu long ou court en fonction du produit β*l (pour les sols cohérents) ou η*l (pour les sols pulvérulents). Le programme permet à l'utilisateur de mettre en œuvre les différents critères pour différents types de pieu proposés dans la littérature. Pour un pieu de longueur intermédiaire, le calcul de vérification considère à la fois les pieux courts et les longs, ensuite le programme choisit automatiquement le résultat donnant la plus faible valeur de capacité portante horizontale Qu.
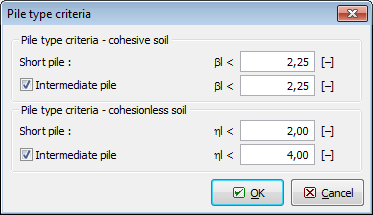 Fenêtre de dialogue "Critère du type de pieu"
Fenêtre de dialogue "Critère du type de pieu"
Le critère du type de pieu (long, court, moyen) est considéré selon les conditions suivantes :
- tête de pieu libre : pieux longs, si β*l > 2,5 ; pieux courts, si β*l < 2,5
- tête de pieu encastrée: pieux longs, si β*l > 1,5 ; pieux courts, si β*l < 1,5
L'installation de la tête du pieu peut être envisagée de deux façons :
- libre - la rotation en tête de pieu n'est pas contrainte
- encastrée - la rotation en tête de pieu est bloquée. Ce cas est typique des pieux d'un réseau de pieux en ligne ou des groupes de pieux.
La résistance du pieu à la flexion est un autre paramètre d'entrée important. Cette quantité est automatiquement calculée par le programme en utilisant la relation :
![]()
où : | Wy | - | module de section transversale [m3] |
f | - | résistance du matériau du pieu [MPa] | |
γk | - | coefficient de réduction de la capacité portante de la section [-] - la résistance de la section est multipliée par différents coefficients de sécurité en fonction de différentes normes et publications, ce coefficient permet au programme d'être adapté à ces normes. |
Pour un pieu en béton armé, la résistance du pieu à la flexion Mu dépend de la quantité d'acier calculée.
Le coefficient de réduction de la capacité portante γQu réduit la valeur totale de la capacité portante horizontale d'un pieu isolé selon la relation :
![]()
où : | Qu | - | capacité portante horizontale d'un pieu isolé [kN] |
γQu | - | coefficient de réduction de la capacité portante [-] |
Le calcul fournit comme résultats finaux : la capacité portante horizontale Qu, sa valeur réduite Qu,red, et la déformation u du pieu à la surface du terrain.
Littérature :
[1] BROMS, BENGT. B.: Lateral Resistance of Piles in Cohesive Soils. Proceedings of the American Society of Civil Engineers, Journal of the Soil Mechanics and Foundations Division, Vol. 90, SM2, 1964.
[2] BROMS, BENGT. B.: Lateral Resistance of Piles in Cohesionless Soils. Proceedings of the American Society of Civil Engineers, Journal of the Soil Mechanics and Foundations Division, vol. 90 SM3, 1964.