Calcul des constantes de Winkler-Pasternak à partir des paramètres de déformation des sols
Les constantes de Winkler-Pasternak C1 et C2 sont calculées à partir de la condition d'égalité des matrices de flexibilité d'une semelle filante infinie et infiniment rigide reposant sur le sous-sol élastique de Winkler-Pasternak.
Le matériau de la couche est caractérisé par les quantités suivantes :
Edef | - | Module de déformation [MPa] |
ν | - | Coefficient de Poisson |
Eoed | - | Module œdométrique [MPa] |
G | - | Module de cisaillement [MPa] |
Parmi ceux-ci, Edef et ν sont indépendants, les deux autres sont déterminés par des relations :
![]()
et
![]()
La largeur de la semelle filante vaut 2b et l'épaisseur de la zone de déformation sous la semelle vaut H.
Par la résolution de la base élastique, nous allons trouver la relation entre le déplacement et la charge de la semelle filante sous la forme :
![]()
où P est la matrice de flexibilité.
En résolvant pour une couche élastique homogène et isotrope sous la ceinture de fondation tout en évitant les déplacements horizontaux, nous obtenons une matrice de flexibilité P de la forme :
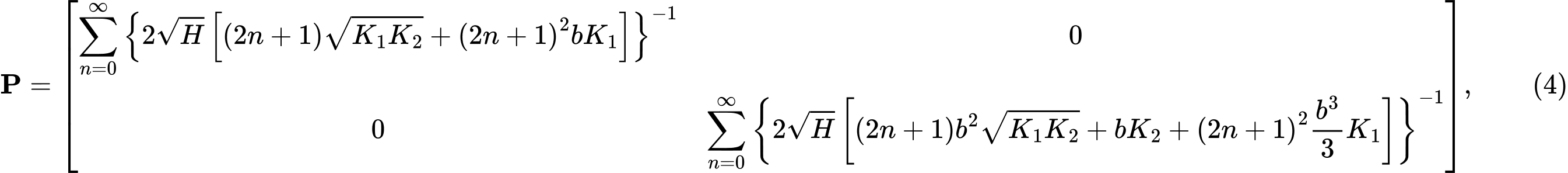
où
![]()
et
![]()
En résolvant l'équation différentielle du modèle de sous-sol à deux paramètres, nous obtenons une matrice P de la forme :
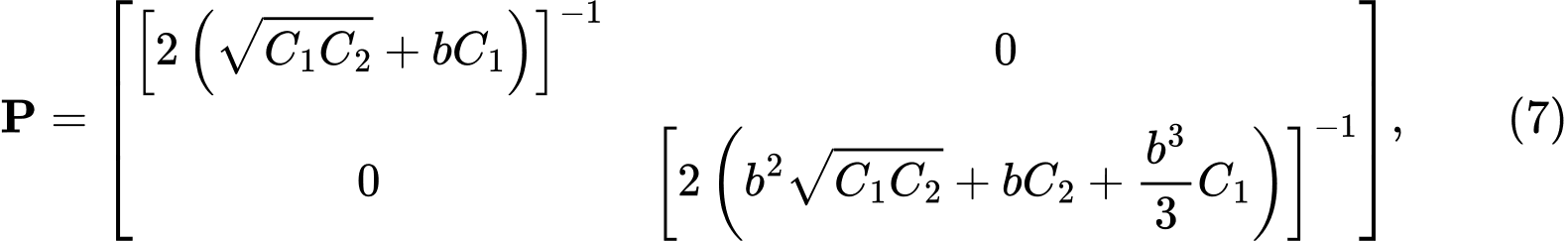
où C1 et C2 sont les constantes du modèle de sous-sol de Winkler-Pasternak. Nous trouvons leurs valeurs à partir de la condition selon laquelle la matrice P de l'expression (4) doit être identique à la matrice P de l'expression (7). Par comparaison et modification, nous obtenons les relations suivantes :
![]()
et
![]()
où
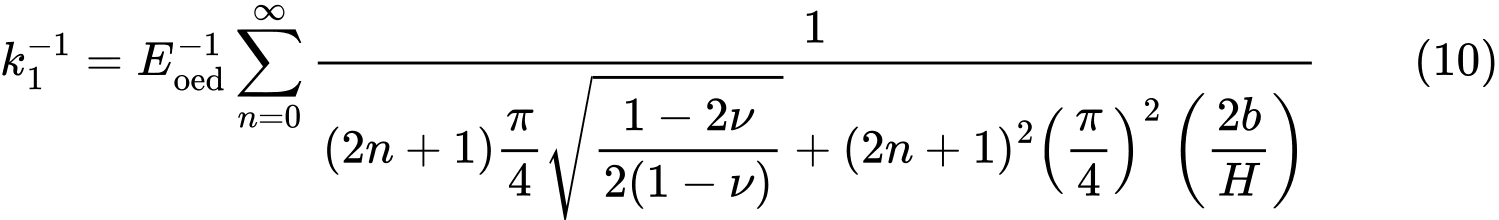
et
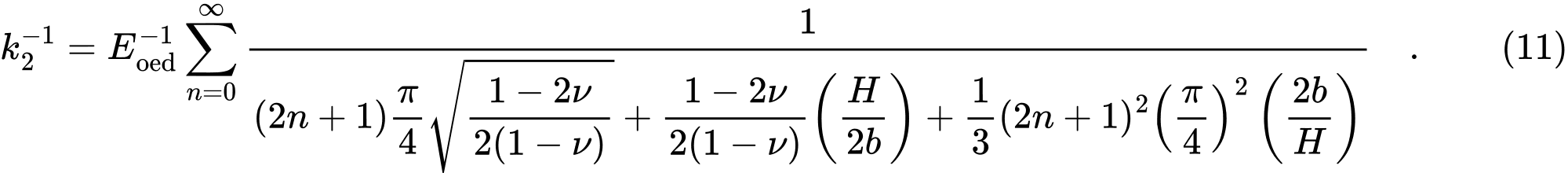
Les valeurs de C1 et C2 sont directement calculées à partir des relations (8) et (9), tandis que les sommes infinies dans les expressions (10) et (11) sont approchées dans Geo5 en considérant les 21 premiers termes.
Littérature: Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984