Schodovitá smyková plocha
Pokud se v horninovém masivu nachází soustava rovnoběžných neprůběžných puklin ukloněných k líci skalní stěny a druhá soustava je nevýrazná, je možné v horninovém masivu uvažovat vytvoření schodovité (zazubené) smykové plochy. Vliv této plochy umožňuje program zavést pomocí teorie Calla a Nicholase, kdy smykový odpor na schodovité smykové ploše se zvýší o hodnotu Δτ:
![]()
![]()
kde: | σn | - | normálové napětí působící kolmo na smykovou plochu |
ν | - | úhel zvlnění | |
T | - | efektivní tahová pevnost schodů z neporušené horniny | |
k | - | část z výšky ht připadající na schody tvořené neporušenou horninou (nevzniklé druhotnou soustavou ploch) | |
ht | - | kolmá výška schodovitého klínu spočívajícího na ploše sklonu hlavní soustavy ploch nespojitosti | |
T0 | - |
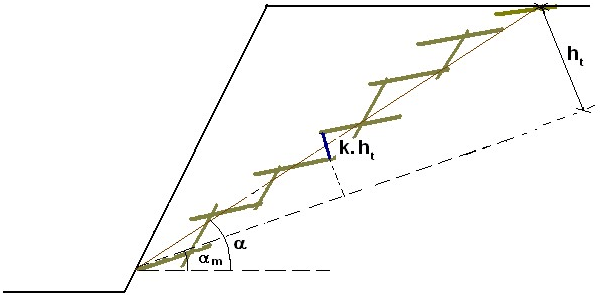 Schodovitá smyková plocha
Schodovitá smyková plocha
Literatura:
W.S. Dershowitz, H.H. Einstein - Characterizing rock joint geometry with joint system models Journal Rock Mechanics and Rock Engineering, Springer Wien ISSN 0723-2632 , Issue Volume 21, Number 1 / January, 1988 Pages 21-51.