Metoda ITF
Metoda ITF je metoda mezní rovnováhy. Vychází ze součtové výminky sil na jednotlivých blocích a neuvažuje momentovou výminku. Princip metody a zavedené předpoklady jsou patrné na obr. 1.
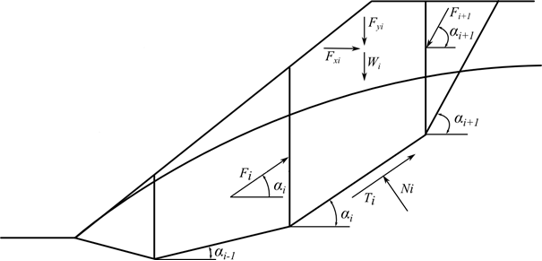Obr. 1 Schéma sil působících na bloku
Působení sil na bloku vychází z následujících předpokladů:
kde: | Wi | - | tíha bloku, pro část bloku, která je pod vodou, se tíha počítá z objemové tíhy nasycené zeminy γsat |
Fyi | - | ostatní svislé zatížení působící na blok | |
Fxi | - | ostatní vodorovné zatížení působící na blok | |
Fi, Fi+1 | - | jsou meziblokové síly, které působí pod úhly αi a αi+1 |
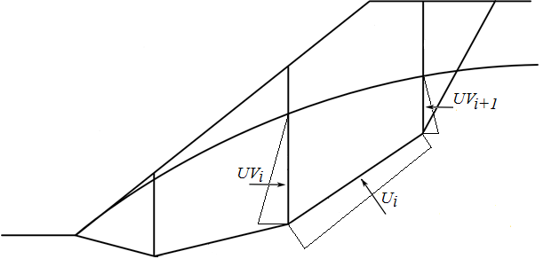Obr. 2 Schéma působení pórového tlaku na blok
Ui | - | výslednice pórového tlaku na úseku smykové plochy | |
UVi,UVi+1 | - | výslednice pórového tlaku na bočních hranách bloku |
Ve výpočtu jsou síly UVi a UVi+1 zahrnuty ve vodorovných silách Fxi.
Ze součtové výminky ve směru kolmém k úseku smykové plochy vyplývá vztah:
Mezi silami na úseku smykové plochy platí vztah:
kde: | φi | - | úhel vnitřního tření zeminy |
ci | - | soudržnost zeminy | |
li | - | délka úseku smykové plochy na i-tém bloku |
Ze součtové výminky ve směru i-tého úseku smykové plochy (pod úhlem αi) plyne vztah pro velikost meziblokové síly Fi:
Dosazením rovnic (1) a (2) do vztahu (3) :
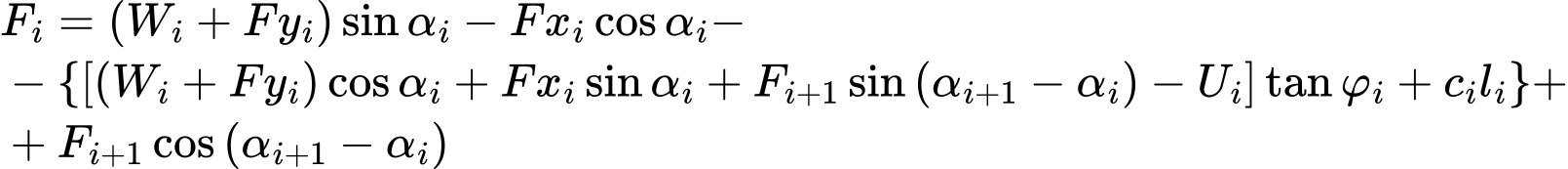
a formální úpravou získáme výsledný tvar výminky rovnováhy:
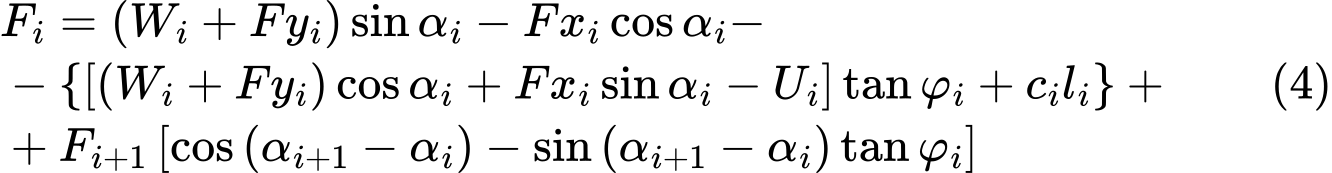
Podmínka rovnováhy bude splněna zavedením stupně stability SF do výpočtu. Stupeň stability se do výpočtu zavede tak, že se jím vydělí charakteristiky pevnosti zeminy c a tanφ. Rovnice (4) pak získá tvar:
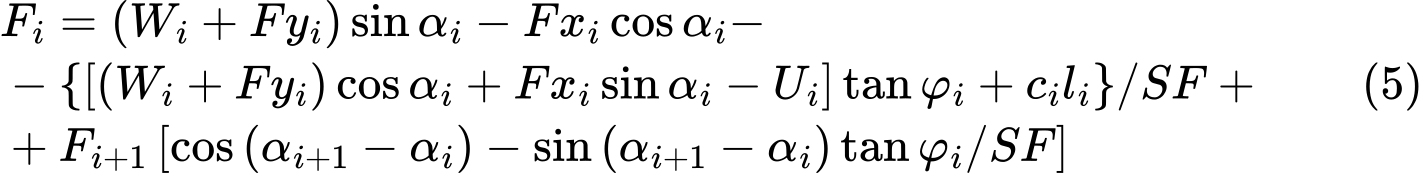
Z rovnice (5) lze následně vypočítat stupeň stability SF, a to iteračním postupem. Iterace probíhá tak, že v nejvyšším (koncovém) bodě smykové plochy se zavede síla Fn o velikosti 0 kN. Pro zvolený stupeň stability SF se pak podle vztahu (5) vypočítají velikosti všech meziblokových sil Fi. Tento postup se opakuje pro různě volené hodnoty stupně stability SF až do chvíle, kdy je nalezen výsledný stupeň stability SF, pro nějž vyjde síla F0 na počátku smykové plochy (u paty svahu) o velikosti 0 kN. Na smykové ploše se počítá s vyloučením tahu. Pokud při výpočtu rovnováhy vychází záporná hodnota normálové síly Ni, což znamená, že zemina je zde namáhána tahem, uvažuje se do dalšího výpočtu nulová hodnota této síly a smyková síla Ti na úseku smykové plochy je stanovena pouze ze soudržnosti zeminy.
Metoda ITF je poměrně citlivá na tvar smykové plochy. Pokud smyková plocha obsahuje ostré lomy, výsledný stupeň stability vychází větší, než odpovídá skutečnosti. Doporučuje se, aby rozdíl sklonů sousedních úseků smykové plochy nebyl větší než 10°. V programu je zabudována kontrola lomů smykové plochy, a pokud je u zadané smykové plochy zjištěn větší rozdíl sklonů sousedních úseků, program zobrazuje hlášení, že výsledky mohou být nadhodnocené. Tento problém zpravidla nenastává u kruhové smykové plochy, ale při použití polygonální smykové plochy je třeba mít tento efekt na zřeteli.
Metoda ITF - explicitní řešení
Explicitní řešení metody ITF spočívá v tom, že je jinak do výpočtu zaveden stupeň stability. Matematické řešení pak nevyžaduje iterační postup, výsledný stupeň stability je spočítán přímým výpočtem. Při explicitním řešení zpravidla vychází vyšší hodnota stupně stability, což může toto řešení někdy zcela znehodnocovat. Zejména v případech, kdy smyková plocha je polygonální a obsahuje ostré lomy.
Řešení vychází z rovnice rovnováhy (4), do níž zavádí stupeň stability SF. Ten je zaveden tak, že se jím násobí aktivní složky sil, to je ty složky, které působí ve směru sesuvu. Podmínka rovnováhy pak má tvar:
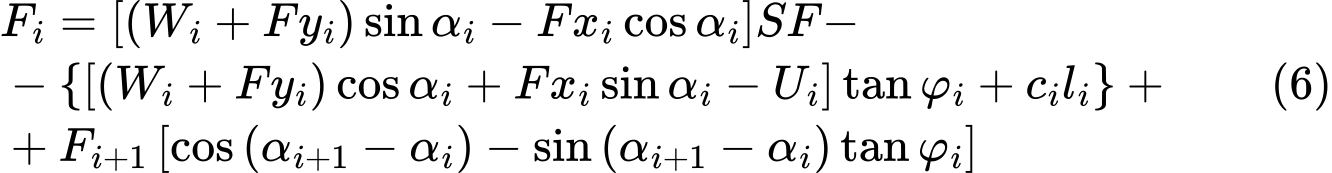
Pro přehlednost zavedeme složku aktivních sil:
dále složku pasivních sil:
a pomocnou funkci:
Rovnici (6) pak lze vyjádřit stručně:
Vyjdeme ze známé hodnoty síly Fn = 0 a sestavíme výrazy pro meziblokové síly F:
Etc….
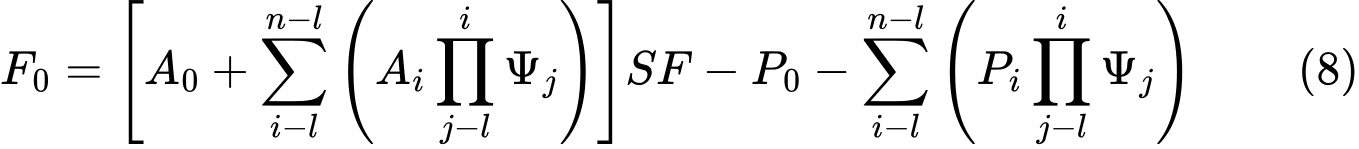
A protože síla F0 na dolním počátku smykové plochy má být rovna 0 kN, lze stupeň stability SF vyjádřit vztahem:
